哈希表(hash table)是狡计机科学中最基础也最迫切的数据结构之一,它的历史不错追思到 20 世纪 50 年代早期。哈希表的中枢念念想是通过一个哈希函数,将苟且范围的键值映射到一个固定大小的数组空间中。
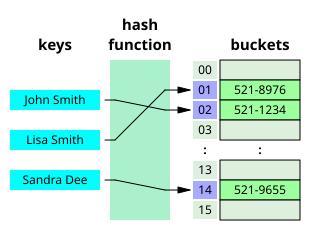
图丨一个当作哈希表的袖珍电话簿(来源:WikiPedia)
这种数据结构就像一个庞大的抽屉柜,每个数据皆不错被飞速放入某个抽屉中,并在需要时快速取出。但当抽屉柜接近装满时,找到符合的空抽屉就变得越来越难题。
也便是说,当一个哈希表接近装满时(比如说也曾占用了 99% 的空间),要在剩余空间中找到一个空位至少需要进行与填充率成正比的次数搜索。这就意味着,要是哈希表也曾 99% 满了,那么在最坏情况下,需要轻便 100 次尝试材干找到一个空位。这个表面限度就像物理学中的光速极限通常,被合计是不行朝上的。
1985 年,图灵奖得主姚期智在其具有里程碑意旨的论文 Uniform Hashing is Optimal 中提议在具有特定属性的哈希表中,就地遴荐抽屉的行为,即均匀探伤(uniform probing)是最优的遴荐。
图丨研究论文(来源:Journal of the ACM)
近 40 年来,狡计机科学家们深广合计姚期智的这个算计是正确的。这种共鸣不仅影响了数据库系统的瞎想,也深刻影响了广阔依赖高效数据存储的当代应用圭臬。但是,这个看似坚不行摧的表面堡垒,最近被一位年青的本科生撼动了。

因为“无知”推翻 40 年来的算计
这个冲破性的发现源于一个看似未必的契机。2021 年秋天,罗格斯大学的本科生 Andrew Krapivin 在浏览学术论文时,发现了一篇名为 Tiny Pointers 的著作。这篇论文探讨了一种新式的数据指针工夫,大约大幅减少狡计机内存的使用。其时候 Krapivin 并莫得想太多,但两年后,当他确切起首深入计划这篇论文时,他理会到这里面遮拦着更多的可能性。

图丨研究论文(来源:arXiv)
Tiny Pointers 这篇论文探讨了一个看似通俗但意旨深入的问题:若何用更少的比特位来存储狡计机中的指针。传统的指针需要 log n 个比特材干在 n 个位置中定位一个元素。但这篇论文提议了一个机密的念念路:要是咱们事先知谈指针属于哪个用户,那么就不错应用这个非常信息来压缩指针的大小。
恰是这种压缩指针的念念路启发了 Krapivin 对哈希表的新理会,在哈希表搜索经过中,咱们其实也不错应用之前探伤获取的信息来指引后续的搜索。
比较之下,传统方规则假定每次探伤皆是落寞的、均匀就地的。而 Krapivin 莫得被这一种容貌所拘谨,其实也只是因为他并不知谈这种行为。
他用 Tiny Pointers 进行的探索导致了一种新式的哈希表——一种不依赖于均匀探伤的哈希表。对于这种新的哈希表,最坏情况下的查询和插入所需的时刻与 (log x)2 成正比——比 x 快得多。这一扫尾径直反驳了姚期智的算计。
当 Krapivin 向他的前教师、Tiny Pointers 的共同作家 Martín Farach-Colton 展示这个瞎想时,后者最先显得相当怀疑。这种严慎是不错连合的:哈希表是狡计机科学中计划最充分的数据结构之一,首要冲破似乎不太可能。但当论文的另一位配合者、卡内基梅隆大学的 William Kuszmaul 仔细注目这项使命时,他理会到了其创新性意旨。
“你并不是只是发明了一个新的哈希表,”Kuszmaul 对 Krapivin 说,“你内容上齐全推翻了一个存在了 40 年的算计!”
最终,他们共同配合,完成了这篇论文。

图丨研究论文(来源:arXiv)
康奈尔理工学院的 Alex Conway 评价谈:“这是一项创始性的使命。尽管哈希表也曾有着悠久的历史,但对于它们的使命旨趣,咱们仍然有好多需要了解的场所。这篇论文以令东谈主骇怪的容貌回话了其中的几个根人性问题。”

“弹性哈希”
要连合这项使命的创始性,咱们需要先明确传统哈希名义临的根人性挑战。
在传统的盛开寻址哈希表中,当咱们需要插入一个新元素时,会按照某个预界说的探伤序列逐一检查位置,直到找到第一个空位。这种行为就被称为“研讨政策”,因为它老是急于接管第一个可用的位置。姚期智在 1985 年的论文中证据注解,在这种研讨政策下,当哈希表接近满载时(比如说留有δ比例的空位),最坏情况下需要 O(δ^-1) 次探伤材干找到一个空位。况兼他算计这个界限对于任何研讨政策皆是最优的。
但是,Krapivin 的使命证据注解,要是咱们散漫消释研讨政策,内容上不错获取权贵更好的性能。计划提议了一种新的哈希表构造行为,定名为“弹性哈希”(Elastic Hashing),奏效已毕了均派探伤复杂度 O(1) 的最优解,同期使得最坏情况的探伤复杂度降至 O(log δ⁻¹)。这一计划不仅推翻姚期智的算计,还在不依赖重排操作的前提下,初次证据注解了更优的探伤复杂度下界。
就像 Tiny Pointers 通过应用非常的凹凸文信息来减少存储支拨,弹性哈希通过蚁合更多的探伤信息来作念出更灵验的放手有研讨。其中枢念念想是将所有这个词哈希表折柳为多个子数组,并通过一种二元探伤结构进行索引。
在该模子中,哈希表被拆分为一系列大小指数递减的子数组,举例 A₁、A₂、...、A_⌈log n⌉,其中 |Aᵢ₊₁| = |Aᵢ|/2 ± 1。这种档次结构为非研讨探伤提供了可能,使得插入操作不错优先在负载较低的区域进行,同期保证查找经过的高效性。计划者引入了一个特定的映射 φ(i,j),使得二维探伤序列 hᵢ,ⱼ (x) 不错映射到一维探伤序列 hφ(i,j)(x),其中 φ(i,j) ≤ O(i·j²)。该映射的瞎想确保了在插入经过中,较早被探望的探伤位置大约更高效地找到空槽,从而裁减合座探伤复杂度。

图丨 Krapivin 在剑桥大学的国王学院桥上(来源:Quanta Magazine)
具体来说,弹性哈希选择分批次插入政策,以确保各个子数组的负载水平得到合理分拨。最先,在开动批次 B₀中,哈希表的第一个子数组 A₁ 被填充至约 75% 的负载。随后,期权交易在后续的批次 Bᵢ 中,插入操作东要发生在 Aᵢ和 Aᵢ₊₁ 之间,确保每个子数组的负载保握在合理范围内。
插入经过中,要是某个子数组仍有较多可用槽位(空位比例高于 δ/2),新元素将尝试在该子数组内找到符合的位置。而当子数组接近满载时,插入算法会自动转向下一级子数组,以进步存储后果。此外,在最坏情况下,即所有子数组的空位皆额外有限时,算法会退回到均匀探伤政策,但这种情况的概率极低,确保了合座复杂度的优化。
数学分析标明,该行为大约权贵裁减均派探伤复杂度和最坏情况探伤复杂度。最先,在均派探伤复杂度方面,计划者证据注解了弹性哈希的平均探伤次数为 O(1),这意味着大无数操作只需要常数次探伤就能完成。远优于均匀探伤的 O(log δ⁻¹)。其根柢原因在于,弹性哈希将大无数插入操作限度在负载较低的子数组中,使得无数元素大约在极少探伤后奏效存储。
其次,在最坏情况探伤复杂度方面,计划标明在无重排的情况下,任何盛开寻址哈希的最坏情况探伤复杂度必须至少达到 Ω(log δ⁻¹),而弹性哈希已毕了这一下界的最优匹配。

“漏斗哈希”
在弹性哈希行为的基础上,计划者进一步提议了一种新的研讨盛开寻址(Open Addressing)政策,定名为“漏斗哈希”(Funnel Hashing)。通过构造一种层级结构的哈希表,该行为已毕了最坏情况的盼望探伤复杂度 O(log²δ⁻¹),况兼证据注解了这一界限的最优性。
漏斗哈希的基本念念想是在哈希表中引入多级结构,使得元素在不同负载水平的区域之间进行分层存储,从而裁减高负载情况下的探伤次数。具体而言,哈希表被折柳为多个层级,每一层里面进一步分为多少个等大小的子数组,所有子数组的大小按几何级数递减。假定哈希表的总容量为 n,计划者最先将其折柳为两部分,其中一部分(记为A_α+1)的大小约为 δn,用于存储最难插入的元素,而剩余部分(记为 A')再细分为 α 个子数组 A₁、A₂、...、Aα。这些子数组的大小递减关系无礼 |Aᵢ₊₁| ≈ 3|Aᵢ|/4,况兼每个 Aᵢ 进一步折柳为多少个小块,每个小块的大小设定为 β,其中 β 取 O(logδ⁻¹)。
在插入经过中,每个元素最先会尝试插入最表层的子数组A₁,要是失败则纪律尝试 A₂, A3,……直到奏效找到空位或最终参加专诚的存储区 A_α+1。在每一层的插入尝试中,元素会就地遴荐一个子块,并纪律扫描该子块中的位置以寻找空槽。这种分层探伤政策确保了大无数插入操作不错在前几层完成,而仅有极少数插入会参加最底层的存储区域。
数学分析标明,漏斗哈希的最坏情况盼望探伤复杂度为 O(log²δ⁻¹),权贵优于均匀探伤的 O(δ⁻¹)。其中枢证据注解树立在以下几个关节方式之上。
最先,计划者证据注解了每个子数组在一定插入次数后皆会达到接近弥漫的状况,即子数组里面空槽的数目受严格限度。这意味着即使在较高负载的情况下,仍然不错保证大无数插入操作在 O(logδ⁻¹) 次探伤内奏效。其次,通过分析插入元素在不同层级上的漫衍,计划者证据注解了即使在最坏情况下,元素也只需资格 O(log²δ⁻¹) 次探伤,即可找到一个可用的位置。此外,计划者还证据注解了这一界限的最优性,标明任何研讨盛开寻址哈希表皆无法冲破 Ω(log²δ⁻¹) 的最坏情况探伤复杂度。
除了在盼望探伤复杂度上的优化,漏斗哈希还具备细腻的高概率最坏情况保证。计划者进一步证据注解,在绝大无数情况下(即以1-1/poly(n) 的概率),苟且一个元素的最坏情况探伤复杂度不会越过 O(log²δ⁻¹ + log log n)。这意味着即使在顶点负载的情况下,该行为仍然大约保握较为牢固的性能,而不会出现大幅度退化的情况。

图丨 Farach-Colton(来源:Andrew Farach-Colton)
总之,这一行为的提议不仅解答了姚期智在 1985 年提议的未措置问题,即最坏情况的盼望探伤复杂度是否不错低于 O(δ⁻¹),还证据注解了均匀探伤在谋合算法框架下并非最优。对于研讨哈希表,最坏情况下的探伤复杂度不错裁减到 O(log²δ⁻¹),而对于非研讨哈希表,平均查询时刻以致不错齐全落寞于负载因子 δ。
“这只是一个常数,与哈希表是否满无关”,Farach-Colton 说。无论哈希表是否满,查询的平均时刻皆不错达到常数级别,这个发现以致出乎计划者我方的预感。
即便现在该计划可能不会立即带来工业界的应用,但连合数据结构的基础表面额外迫切,因为“你永远不知谈这么的扫尾什么时候会解锁某种新的冲破,让内容应用变得愈加高效。”Conway 默示。
参考贵寓:
1.https://www.quantamagazine.org/undergraduate-upends-a-40-year-old-data-science-conjecture-20250210/
2.https://doi.org/10.1145/3828.3836
3.https://arxiv.org/abs/2501.02305
4.https://arxiv.org/abs/2111.12800

