猫猫和东说念主的交互行径,居然被物理学家用方程式写出来了!
其效果还隆重刊登在了《好意思国物理学杂志》上。

缘由即是这位名叫Anxo Biasi的小哥,有一天不雅察起了自家猫猫,突发奇念念:能否将猫视为一个在东说念主产生的势场中教导的质点,用物理方程来态状其行径?
收尾通过仔细研究,他得胜构建了一个概况定性重现多种猫与东说念主交互行径特征的猫猫教导方程。
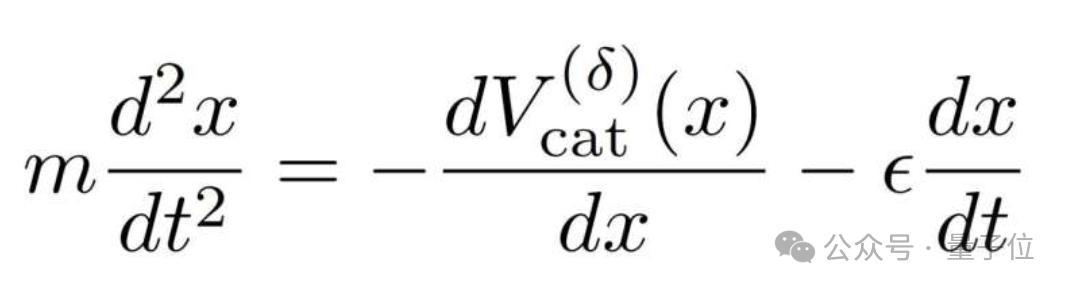
此前天然物理学家仍是研究过猫的一些性情(比如猫总能四脚着地的智商) ,还有下图这种用来态状猫越小越可儿的“黑洞猫”幽默比方。
但这项研究是初度以方程的时事对猫的典型行径特征进行建模。
致使猫猫在夜间纵容跑酷也被再现了。
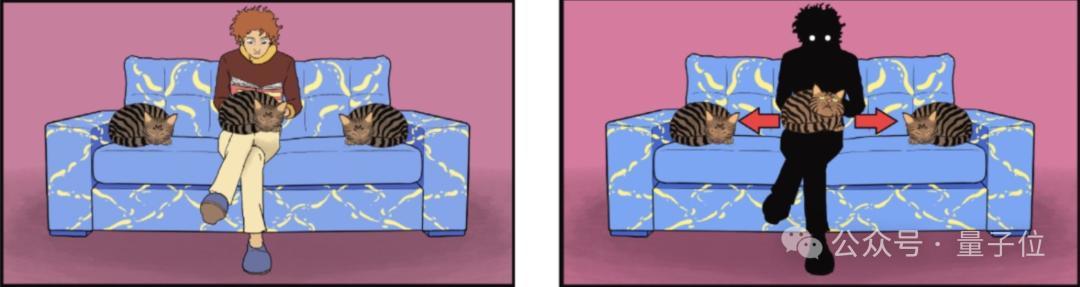
还有猫猫闲居会对主东说念主的招呼爱答不睬,它们会在最可爱的东说念主的腿上待更久……
趴在主东说念主腿上VS趴在目生东说念主腿上,be like:
网友们以为甚是情理,匡助宇宙领会一些经典力学认识的例子+1。
真没念念到爱猫东说念主士会作念到如斯地步。
猫教导方程,怎么开拓?
这位小哥将猫猫建模为一个点粒子,早先议论日常不雅察以及多样接洽中界说了猫猫的7种常见场景。
(点粒子,物理学中一种粒子理念念化态状,主要特色是不占用空间。举个例子,唯一离得够远,多样形式的物体齐会看似于一个点。)
明确指出的是,这是一项表面研究,莫得进行动物践诺,通盘论断齐开拓在日常不雅察和物理建模的基础上。

这次关注的是猫与东说念主互动的一个浅显场景:一只猫和一个静止的东说念主在整个。
这7种行径差别是:
P1:猫休息时闲居会与东说念主保捏一定距离。
P2:当猫趴在东说念主身上休息时(如趴在腿上、肚子上、背上),极小的刺激就可能使它们离开这个位置(如一只苍蝇、一个难以察觉的声息、相近星系原子的β-衰变)。产生离开所需的扰动强度取决于猫对其所依靠的东说念主的依恋进度。
P3:当猫被东说念主抚摸时,它们会前后舞动。
P4:当猫被东说念主招呼时,它们很少回复。
P5:当猫决定接近招呼它们的东说念主时,它们往往会在途平分神,无法到达对方身边。

P6:晚上,猫咪会轻佻在房子里跑酷。(这种情况被称为 “zoomies”)
P7:当猫可爱被东说念主抚摸时,它们会发出呼噜声(发出柔和振动的声息)。
天然,这些行径并不具有宽敞性。有些猫也可能推崇得不太彰着。
界说完之后进行研究假定:猫的行径就像它们感知到东说念主周围有一种力。
看成初步访佛,他们将猫的能源学模子界说为在存在外部势能(由静止的东说念主引起)和摩擦项的情况下,一个效率牛顿力学的点粒子。
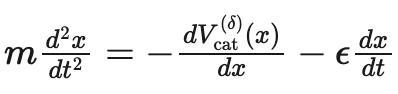
其中x(t)默示猫在手艺t相干于位于x=0处的东说念主的位置,m>0是猫的质地,何况ϵ>0是摩擦总计,其值取决于每只猫。
将微分方程改革为基于有理函数的时事。它提供了对均衡点的截止,这么解决均衡点的数目、相对位置和平定性。
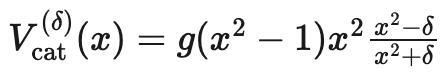
其中,g>0是耦合常数(从目下起将g简化诞生为g=1,但这不会改变模子的定性图像);δ在[0,1]区间,反馈了猫对东说念主的依恋。
当δ=0 时,点x=0(东说念主的位置)是不屈定的:猫对东说念主莫得依恋。
当δ>0时, 点x=0是平定的。何况δ值越大,猫的依恋越强。当δ=1时,这标明猫对东说念主有很强的依恋。
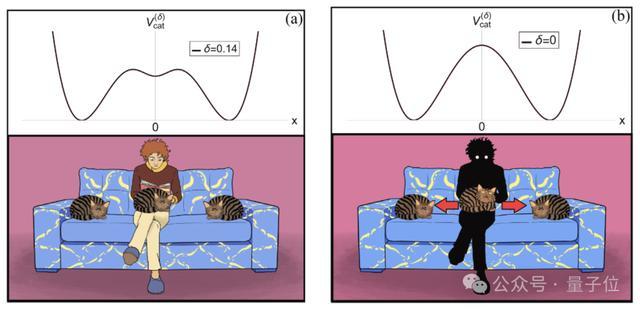
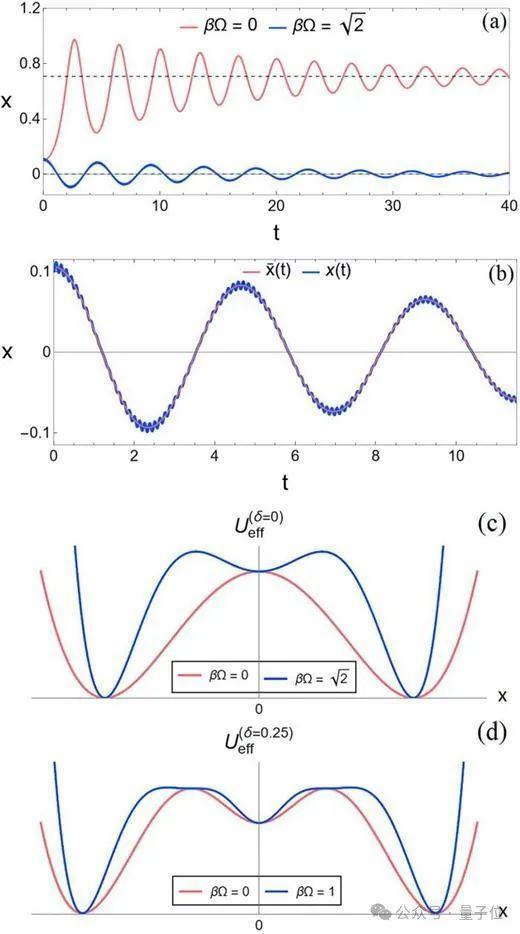
图1:(a)猫依附在东说念主身上,(b)东说念主对猫来说十足是目生东说念主。这两种情况猫齐处于静止状况,处于三个均衡点。
此外,需要公式 (1) 中的摩擦项来减少能量。不然,猫在行径一段手艺后就不会趋于静止状况,比如傍边两侧∞状况。
为了阻难猫的教导,需要ϵ≥0,而且摩擦力必须与速率的奇数次方成正比。
终末要细心的是,猫是在三维空间中迁移的。然则,由于最关键的参数是猫和东说念主之间的距离,咱们假定猫沿着一条线迁移,这进一步简化了分析。
还将跑酷和发出呼噜声模拟出来了
基于猫教导方程,小哥将猫的7种行径定性地默示了出来。
P1:猫咪休息时闲居会与东说念主保捏一定距离。这种行径被中心外的全局最小值所捕捉。

如图1所示,猫可能以不同的速率从很多位置运转,但由于摩擦项,最终会到达最小值。
在大大批情况下,最终位置将是全局最小值,相配是关于猫和东说念主之间的弱关系(δ较小时)。
当δ趋近于1时,小麦财经股票配资x=0将成为极度的全局最小值。
P2,该述说的第一部分由势能均衡点x=0(东说念主的位置)重现,因为猫可能靠在东说念主身上。
该述说的第二部分是通过势能对δ的依赖性来捕捉的。也即是说当δ=0时, x=0是不屈定的,这标明在职意小的扰动下,猫齐会偏离东说念主。跟着δ的增长,需要更强的刺激才调将猫从东说念主身上分离。
P3, “当猫被东说念主抚摸时,它们会以飘浮教导来去迁移。” 这种效应也在x=0隔邻的平定区域重现(关于δ>0的情况)。
当猫闲隙地围聚东说念主(动能低)时,它们会围绕东说念主进行小幅度的飘浮,并不断到静态,这归功于方程中的摩擦项。
即使被目生东说念主抚摸(δ=0),猫也可能推崇出这些平定的飘浮,但为此必须添加一个新变量(呼噜声)。
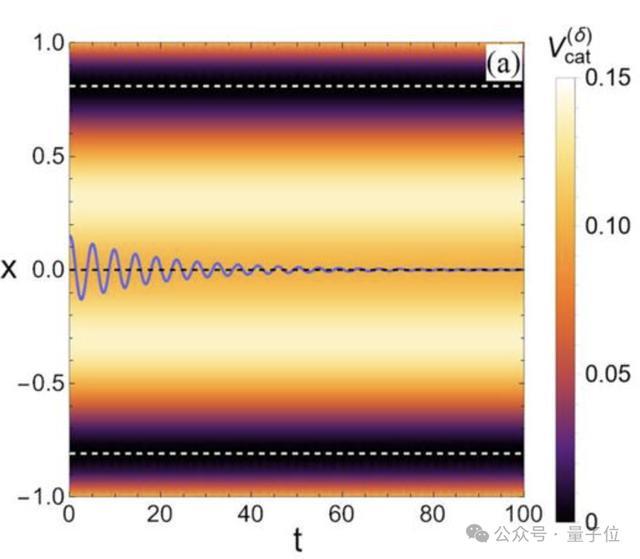
不雅察收尾P4和P5不错用偏心最小值与东说念主(x=0)之间的势垒来解说,如图1所示。
P4被招呼的行径被建模为猫向东说念主发出的冲动,这会导致动能增多,这种能量注入可能足以或不及以克服势垒。由于能量不及,猫会在一段手艺后,再次不断到静止位置。
如下图蓝色(较暗)和绿色(较亮)轨迹所走漏。
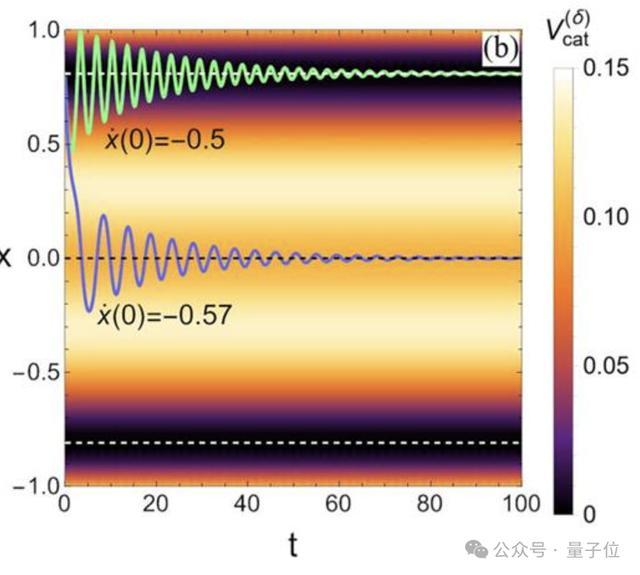
当猫受到迷漫强的刺激(冲动)接近东说念主时,也就来到了P5:“当猫决定接近招呼它们的东说念主时,它们频频在途平分神而无法接近东说念主。” 这一不雅察收尾也用上图绿色(较浅)轨迹所示。
这一阵势中,猫的质地也会起作用(Doge), 猫得回的速率会跟着质地的增多而减小——
体重较轻的猫(举例小猫)会推崇出龙马精神的动作并对任何刺激作念出反应,而体重较重的猫(举例老年猫或喂食过度的猫)则不会推崇出相同的柔柔。这也与不雅察收尾彰着一致。

除此除外,作家还将这一方程进行了拓展:猫猫跑酷和呼噜声,这两种行径也被重现了。
猫猫跑酷。
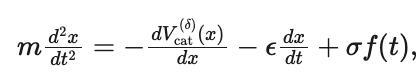
其中σ为常数,f (t) 为外部随即免强。在给定手艺内产生快速迁移的概率取决于摩擦力ϵ和免强σ的值。
这使咱们概况凭证每只猫的特殊性调养模子。举例,小猫赓续推崇出这些时代,对应于较低的摩擦力和较高的免强力,而老年猫则很少推崇出这种行径。
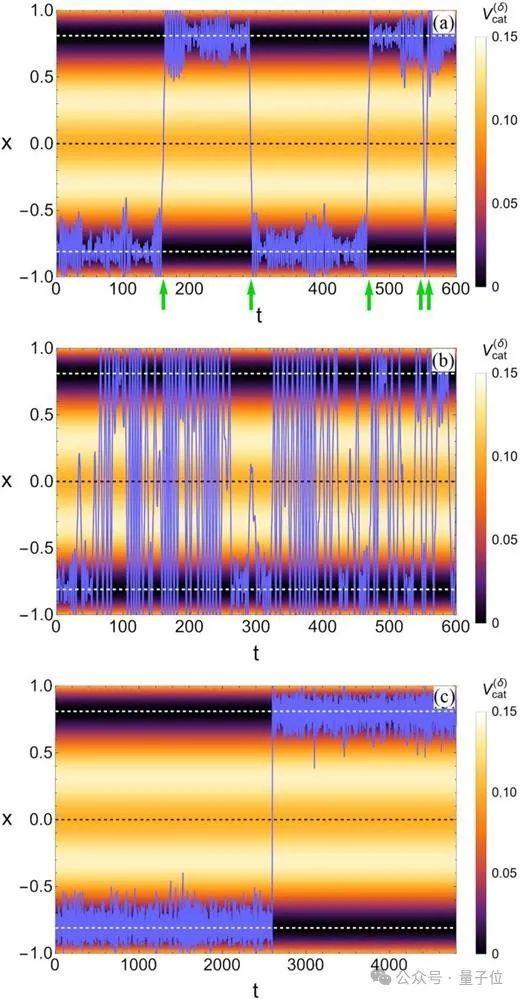
(a)走漏猫可能短暂从一个均衡点跑到另一个均衡点,在哪里停留一段手艺,然后再次随即地回到上一个均衡点。(b)为小猫(c)为老年猫
关于第7种行径,作家界说呼噜声是一种平定机制。
一部分原因在于当猫被抚摸并运转发出呼噜声时,东说念主们闲居会有连续抚摸猫的冲动,从而通过这种面貌增强了流程的平定性。
以卡皮察摆看成类比,猫在发出呼噜声时会振动,振动不错看成不屈定均衡点的平定机制,由此界说猫猫呼噜声教导模子:
振动不错加强猫与东说念主之间的灵验关系。

在原有猫方程基础上,引入了外部振动免强来模拟这种效果。
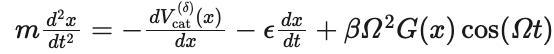
其中G (x) 暂时为无顾问函数,β和Ω差别为猫中振动的振幅和频率。此类驱动项模拟了在手艺飘浮场中迁移或受到周期性免强的粒子。
好了,此举从物理学的角度探索了猫与东说念主之间的互动。
作家默示,这种互动模子旨在用于经典力学的初学课程,让学生更好地老练均衡点、势垒、摩擦或外力等认识。
灵感来自于自家的猫猫
这次研究效果来自表面物理学家Anxo Biasi和他家的猫猫Eme。

他主要研究非线性演化方程的动态行径,相配关注奇异点的酿成、始终动态行径和湍流问题,这在流体能源学、玻色-爱因斯坦凝华态和广义相对论等规模具有世俗欺诈。
Anxo此前通过巴黎高档师范学院物理系的La Caixa后生首长计议,加入了加利西亚高能物理研究所(IGFAE)。
在IGFAE,他仍是完成了博士论文,并将加入弦表面关系规模的研究团队,连续研究物理学和数学交叉规模的非线性演化方程。

开拓猫教导方程,早先源自于他在愚东说念主节的一个念念法:念念找一种对学生更有劝诱力的情理面貌来解说物理。
他本东说念主的猫猫Eme给了他灵感,通过仔细不雅察Eme与他互动时的行径,Anxo发现这种行径模式具有重迭性和可揣摸性,于是运转我方尝试用物理模子来态状这些行径。

渐渐地,这一在某种进度上看似是开打趣的事情,呈现出了学术形态。
为此在致谢中还挑升感谢了Eme。

这项使命还不错延迟到多样场景,除了不错从物理学角度探索猫与东说念主之间互动其它特征,还不错探讨猫与猫、狗与狗或狗与东说念主之间的互动。
好念念知说念猫猫打架是什么方程哇~


